AGC027C ABland Yard

发表于 | 分类于

Description

有一个\(n\)点\(m\)边的点权为\(0/1\)的无向图，对于每条路径（可以是非简单路径），我们称它生成的字符串为把经过点的点权按经过顺序排列所得的序列。

请问，这个图是否可以生成所有01串？

\(1\leq n\leq 2\times 10^5, 2\leq m\leq 2\times 10^5\)。

Solution

不难发现，如果要搞出所有序列的话，图中必然有这种构造：

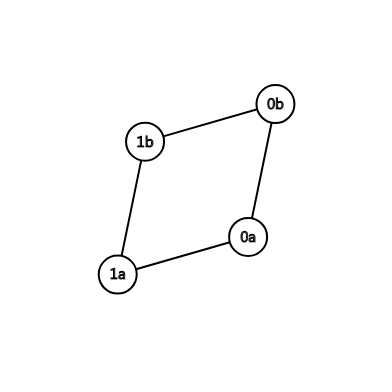
这里面a和b只是为了区分不同的点，数字才是点权。其中同权点间加一条边可以改成自环辣~

然后接下来的问题在于怎样判定这个图是否包含这个构造……我们可以尝试每次在图中删除相邻点颜色都相同的点（或者零度点），如此下去如果图最后还是有点的话很显然就会有这种构造了。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <functional>
#include <utility>
#include <vector>
#include <queue>
const int maxn = 200005;
std::vector<int> G[maxn];
int typ[maxn]; int deg[maxn][2];
inline void add_edge(int u, int v) {
  G[u].push_back(v);
}
inline void ins_edge(int u, int v) {
  add_edge(u, v); add_edge(v, u);
  deg[u][typ[v]] ++; deg[v][typ[u]] ++;
}
 
bool can_del(int x) {
  return (deg[x][0] == 0 || deg[x][1] == 0);
}
bool vis[maxn]; int n;
bool check() {
  std::queue<int> Q;
  for(int i = 1; i <= n; i ++) {
    if(can_del(i)) {
      Q.push(i); vis[i] = true;
    }
  }
  int cnt = 0;
  while(!Q.empty()) {
    int u = Q.front(); Q.pop(); cnt ++;
    for(int v : G[u]) {
      deg[v][typ[u]] --;
      if(!vis[v] && can_del(v)) {
        Q.push(v); vis[v] =  true;
      }
    }
  }
  return (cnt < n);
}
 
char buf[maxn];
int main() {
  int m; scanf("%d%d", &n, &m);
  scanf("%s", buf + 1);
  for(int i = 1; i <= n; i ++) typ[i] = buf[i] - 'A';
  for(int i = 1; i <= m; i ++) {
    int u, v; scanf("%d%d", &u, &v);
    ins_edge(u, v);
  }
  if(check()) {
    puts("Yes");
  } else {
    puts("No");
  }
  return 0;
}